虚拟 — 膨胀出全息世界
“许多独立的并且很有说服力的论点,都表明时空这个概念本身并不是基础性的。时空注定要消亡。在物理定律的实际底层描述中,根本不存在时空这样的东西。这是非常令人震惊的,因为物理学被认为是描述在空间和时间中发生的事情。因此,如果没有时空,就不清楚物理学讲的什么。” — 尼马·阿尔卡尼-哈米德,康奈尔大学信使讲座,2016
时空和物体感知的新视角
科学可以揭开奇异事物的神秘面纱。这种天赋带来了新技术——从手机到卫星。用亚瑟·克拉克的话说,这些技术看起来“和魔术没什么两样”。
科学也可以让平凡显得神秘。它可以突然把我们扔进好奇的兔子洞。例如,我看到一把勺子现在就放在那边的桌子上。这是如此稀松平常,以至于我根本不想花时间去思考它。但是就在这里,在完全出乎我预料的地方,科学注入了深奥的神秘:我们仍然不理解“现在”和“那边”。也就是说,我们不理解时间和空间——长度、宽度和深度——这些我们认为理所当然的东西,它们交织在我们日常感知的最根本结构中,我们认为它们是真实可靠的物理实在指南。
现在许多物理学家告诉我们,我们知道的是,时空注定消亡。空间和时间在我们的日常感知中占据中心地位。但是,即使是爱因斯坦精心构造的时空,也不能真正描述自然的基本定律。时空,以及它所包含的所有物体,在那个真实的描述中将会消失。例如,诺贝尔奖得主大卫·格罗斯注意到:“每个研究弦理论的人都相信……时空注定消亡。但我们不知道它会被什么取代。” 菲尔兹奖得主爱德华·威滕也认为时空可能“注定消亡”。普林斯顿高等研究院的内森·塞伯格说:“我几乎可以肯定,时间和空间都是错觉。这些原始概念都将被更复杂的东西取代。”
这令人深感不安。正如这一章开头引用的阿尔卡尼-哈米德的解释,“物理学被认为是描述在空间和时间中发生的事情。因此,如果没有时空,就不清楚物理学讲的什么。”对物理学家来说,这是个好消息。承认一个理论的失败,无论这个理论多么珍贵,都是一种进步。对于具有创造性的理论家来说,用更基本的东西取代时空理论是令人兴奋的挑战,很有可能改变我们对世界的看法——也许这是我们第一次有机会搞清楚,物理学到底讲的什么。
我在这一章的目标并不那么雄心勃勃。对时空注定消亡的认识以及随之而来的东西,还没有为目前的视觉理论提供启示。这些理论一般都假设空间和时间中的物体是物理实在的基础,视觉一般能复现这些预先存在的物体的真实属性。对于哪些真实属性被呈现,以及呈现是如何生成的,目前的感知理论普遍都还不能达成一致,但它们都假定物理学家认为错误的事情是正确的——时空中的物体是基础性的。
我将简要讨论感知的标准理论,然后给出一个关于我们对时空和物体感知的新视角。这个新的视角是受感知界面理论(ITP)和全息原理启发——在第 6 章中讨论的关键发现,即一个空间区域中可以存储的数据量取决于该区域外围的面积,而不是体积。这种关于时空和物体的新视角源于这样一个想法,即我们的感知已进化到编码适应度收益,并引导适应性行为。时空和物体的用途正在于此。但是怎么做到的呢?我认为部分是通过数据压缩和适应性信息纠错。
数据压缩和适应性信息纠错
先看看数据压缩。适应度收益函数可能很复杂,而且有许多适应度收益函数都会关系到人的生存,因此与人有关的适应性信息的量可能非常庞大——如果人必须全部感知的话将是沉重的负担。因此人需要把它压缩到可以处理的水平。
假设你想通过电子邮件将度假照片发送给朋友,但是图像超过了邮件服务器允许的大小。你可以压缩图像并检查清晰度是否可接受。如果不行,看不清你的家人在大峡谷的留影,你就不要压缩太多。你寻找一个可接受的折中方案——压缩到可以发送,但又不会模糊到不值得发送的程度。
对于人类视觉,时空和物体就是一种可接受的折中。适应度收益函数可以有数百个维度。经过亿万年的自然选择塑造,人类视觉把这些维度压缩成三维空间和一维时间,压缩成用形状和颜色维度刻画的物体。人不能处理数百个维度,但还是能处理一些。压缩过程无疑略去了一些适应性信息。例如,我们没有看到每天有数以百万计的 μ 介子穿过并用电离辐射破坏我们的身体。但我们还是感知到了足够多的关于生存和繁育后代的适应性信息。
我们在三维空间中看到物体,并不是因为我们重构了客观实在,而是因为这是一种压缩格式,这种压缩算法是进化赋予我们的。其他物种可能有不同的表示适应性的数据格式。我们的生活、移动和存在,并不是在时空和物体组成的客观实在中,而是在时空和物体格式的数据结构中,这种数据结构在智人中进化出来,以一种节约和有用的方式来表示适应度收益。我们的感知被编码为这种数据结构,而我们则错误地认为它的时空格式就是我们生活在其中的客观实在。这个错误是可以理解的,也是可以原谅的:我们的数据格式不仅限制了我们感知的方式,还限制了我们思考的方式。挣脱它的限制,甚至认识到这种可能性,都不容易。对这种可能性的领悟在知识阶层和宗教文化中有悠久的历史。
对于将时空和物体作为适应值的压缩编码,还有很多需要探索。例如,什么样的适应性被空间捕获,什么被物体捕获?形状、颜色、纹理和运动是如何在对适应度的压缩中产生的?为什么适应度的压缩会让我们产生不同形式的感知——视觉、听觉、味觉、嗅觉和触觉?也许空间距离意味着获取资源的成本:一个只消耗几卡路里的苹果可能出现在仅 1 米远的地方,而一个需要更多卡路里的苹果可能出现在更远的地方。猛兽为了抓到我消耗的卡路里越多,它们可能就显得越遥远。最近的实验支持这个观点。例如,丹尼斯·普罗菲特与合作者发现,饮用含糖饮料的人比饮用不含糖饮料(以及人工甜味剂)的人估计的距离要短;经常运动的人比不健身的人估计的距离要短。这表明,我们对距离的感知不仅取决于能量消耗,还取决于能量消耗与我们可用能量的对比。
再来看纠错。当我们使用网上银行或上网购物时,有价值的数据就会通过互联网传播。为了防止被黑客窃取,数据会加密。但另一个同等重要的问题是噪声。假设你花了 60 美元在网上给妈妈买花。后来你发现由于网络噪声小数点滑了两位,你实际上花了 6000 美元——这是一个代价高昂的错误。如果这样的错误很常见,电子商务将无法进行。为了防止这种情况,数据在发送前会被格式化为纠错码。
校验和纠错的关键是冗余。一个简单的例子是重复。假设您想要发送 4 比特数据,例如位串 1101。你可以连续发送三次:110111011101。接收器检查三次传输是否一致。如果一致,它就认为没错。但如果某次传输不同于其他,它就检测到了一个错误。它可以要求重新传输,或者假设相同的两个位串是正确的。
有许多巧妙的方法可以增加冗余,比如将消息嵌入高维空间中。但关键在于,我们的感官传递了关于适应度收益的信息,而获得正确的信息对于生存至关重要。适应度收益的小数点滑一位,对你可能是生与死的差别。可以想见,自然选择会在我们的感知界面中设置冗余,它塑造了我们的时空桌面和物理对象图标,使其带有适应度收益的冗余码,从而可以校验和纠错。
这正是贝肯斯坦和霍金对时空的发现。时空有冗余。二维可以包含任何三维空间中的所有信息。这就是我们在上一章讨论的苏士侃和特胡夫特的全息原理。这不符合直觉,并且违背了我们的假设,即三维空间是我们的感官重建的客观实在。但如果你认同我们的感官呈现适应度,并且需要冗余(比如额外的空间维度),以确保它们的呈现不会受噪声干扰,那么这就说得通了。
物理学家已经证实了自然选择的预测,即空间有冗余。但是,他们是否也证实了这种空间冗余的确有纠错码的功能?这一努力正在进行中,而且很有希望。物理学家阿迈德·阿尔梅赫利、董希和丹尼尔·哈洛发现,全息原理揭示的空间冗余表现出了纠错以防止数据被噪声擦除的特性。如他们所说,“全息原理也自然呈现于一个普遍性命题之中,即对于给定编码能保护多少量子信息不被擦除存在上限。”物理学家约翰·普雷斯基、丹尼尔·哈洛和费尔南多·帕斯陶斯基等人已发现了将时空几何解释为量子纠错码的具体方法。
由此得出的结论是,时空和物体是我们的感官用来呈现适应性的编码。像任何可用的编码一样,它使用冗余来抗噪。这个结论正是感知界面理论,同时增加了额外的洞察,即界面压缩数据和抑制噪声。
我们为什么看到对称性
这个结论还没有得到大多数视觉科学家的认可。他们仍然认为视觉是真实的,重建了时空中真实的物体。加州大学洛杉矶分校医院前首席精神病医生路易斯·韦斯特在《大英百科全书》的“空间感知”条目中阐述了这一假设。韦斯特认为,真实感知是“对存在的刺激的直接感知。没有一定程度的关于物理空间的真实性,人们就不能寻找食物,逃离敌人,甚至不能社交。真实的感知也会让人将变化的刺激体验为好像是稳定的:例如,即使老虎靠近时的感官图像变大了,人们还是倾向于认为老虎的体型保持不变。”
当然,视觉科学家并不声称感知始终是真实的。他们承认通过启发可以扭曲实在。但是他们认为真实性是目标,而且通常可以达到。
例如,他们认为,我们对物体的感知的对称性揭示了客观实在的对称性。视觉科学家齐格蒙特·皮兹洛就是这么说的。“想想动物身体的形状。绝大多数是镜面对称的。我们怎么知道它们是镜面对称的?因为我们把它们看成这样。除非两个对称的半体被认为具有相同的形状,否则就不可能把镜面对称的物体看成镜面对称。请注意这是很让人吃惊的,因为:(1) 我们只看得到前面,两个半体的可见表面;(2)我们从观察方向看到的两个半体相差 180°。除非形状不变性是一种真实的现象,并且除非它接近完美,否则我们甚至不知道对称形状是否真正存在。”
我们可以将这个说法精确化:我们感知中的任何对称性都意味着客观实在中的相应对称性。
这种说法成立吗?这里我们不能依靠直觉,我们需要证明。我们也的确有一个。由我提出猜想并由奇坦·普拉卡什证明的“对称性发明定理”揭示了这种说法是错误的。这个定理指出我们的感知中的对称性并不意味着客观实在的结构。对此的证明是建构性的。它明确展示了在一个没有任何对称性的世界里,感觉和行为是如何拥有对称性的,例如平移、旋转、镜面和洛伦兹对称。
这就提出了一个显而易见的问题。我们看到许多对称的物体。为什么?如果感知的对称性并不意味着实在的对称性,那么我们为什么要看到对称?
答案依然是数据压缩和纠错——它们的算法和数据结构往往涉及对称性。过多的适应度信息可以利用对称性压缩到可接受的水平。为了感受这一点,想象看一个苹果。如果你稍微向左移一点,看起来会怎么样?你可以用对称——简单的旋转和平移——来回答这个问题。你不用为每个视角存储数百万数据,你只需要 5 个——3 个用于平移,2 个用于旋转。对称是我们用来压缩数据和纠错的简单程序。我们感知中的对称揭示了我们如何压缩和编码信息,而不是客观实在的本质。
“但是,”你可能会反对,“我们可以构建计算机视觉系统来驾驶汽车,并且看到和我们一样的形状和对称性。这难道不表明,我们和计算机都看到了实在的本来面目吗?”
并非如此。对称性发明定理适用于任何感知系统,无论是生物还是机器。计算机看到的对称性并不意味着客观实在的结构。我们可以制造一个能看到我们所看到的对称性的机器人。但这并不能让我们洞察世界的结构。
皮兹洛认为进化为对物体和空间的真实感知提供了理论基础。“如果不能提供计划性和目的性行为,动物的成功进化和自然选择的成功将是不可想象的。” 他认为,我们在狩猎、种植和采集方面的成功取决于计划和协作,而这需要对客观实在的真实感知。
计划和协作对我们的成功至关重要。但是,它们需要客观实在的真实呈现吗?根据“事实胜过真理”(FBT)定理,不需要。网络游戏《侠盗猎车手》让玩家为一些不光彩的目标而合作,比如抢劫商店或偷车。他们的计划不是基于对晶体管和网络协议的真实感知,而是基于一个由高速汽车和诱人目标组成的虚假世界。
支持真实感知的论证并不成立。而这个理论却依然是视觉科学的标准理论。根据这一理论,在时空中确实存在具有客观属性 (如形状)的三维物体,即使在没人观察的情况下也存在。当你看苹果时,苹果表面反射的光会被你眼睛的光学器件聚焦到你的二维视网膜上。这个苹果在二维视网膜上的光学投影会丢失苹果的三维形状和深度信息。你的视觉系统会分析它的二维信息,计算出苹果真正的三维形状。它恢复或重建光学投影丢失的信息。这个重建过程有时被称为“逆几何光学”,有时被称为“贝叶斯估计”。
具身认知理论的支持者反驳了这个观点,这个理论建立在心理学家詹姆士·吉布森的思想基础上。他们认为,我们是用真实身体与真实物理世界互动的物理存在,我们的感知与我们的行为紧密联系在一起。感知和身体行为必须放在一起理解。当我看到一个红苹果,我不仅仅是在解决一个逆几何光学或贝叶斯估计的抽象问题,而是看到一个与我的行动紧密关联的三维形状——我如何走向它,抓住它,然后吃掉它。大多数赞成逆几何光学或贝叶斯估计的视觉科学家都同意,行动和感知是紧密关联的。
“激进具身认知”的支持者则主张,感知和行为不仅相互关联,而且感知不需要信息处理。他们认为,感知和行为的互动不用计算和表征也可以理解。这种激进观点的支持者不多,并与量子物理学家主张的所有物理过程都是信息过程,以及信息永远不会被摧毁的观点相矛盾。这种主张也与另一种众所周知的真理不相一致,即任何经历一系列状态转换的系统都可以被解释为一台计算机(也许是一台愚蠢的计算机,但仍然是计算机)。
感知界面理论反对认为感知是真实的标准理论,但同意感知和行为是紧密关联在一起的。我们的感知进化是为了引导适应性探索和行为:我的苹果图标引导我选择吃还是不吃,以及如果吃的话怎么抓和咬;我的毒藤图标引导我选择不吃,以及为了避免任何接触而采取措施。
因果关系是虚构
感知界面理论对因果关系作出了一个违反直觉的断言:时空中物体之间因果关系的出现是虚构的——是有用的虚构,但仍然是虚构。我看见母球把 8 号球打进角袋。我很自然地认为,是母球导致了 8 号球滚向角袋。但严格来说,我错了。时空只是特定物体的桌面,物体是桌面上的图标;或者,就像我们讨论过的,时空是信道,物体是关于适应性的信息。如果我将文件图标拖入回收站,文件会被删除,如果我认为将图标拖入回收站导致了文件被删除,这种认识有助于操作,不过是错的。事实上,通过这种伪因果推理来预测行为后果的能力是界面设计良好的标志。
感知界面理论的这个预测——时空中物体之间因果互动的出现是虚构的——得到了缺乏因果顺序的量子计算的有趣支持。通常我们以特定的因果顺序每次计算一个步骤。例如,可以从数字 10 开始,除以 2,再加 2,得到结果 7。如果我颠倒顺序,先加 2 再除以 2,得到的结果是 6。运算的顺序很重要。但是量子计算机可以没有明确的运算因果顺序。这种计算机利用因果顺序的叠加以实现更高效的计算。
界面理论预测物理因果是虚构的。这与物理学并不矛盾。如果像物理学家现在认为的那样,时空注定消亡,那么其中的物理对象和它们表面上的因果关系也注定会消亡。目前的意识理论也注定如此,例如朱利奥·托诺尼的整合信息论(IIT)或约翰·塞尔的生物自然论,这些理论认为意识具有时空中物理系统的某些因果属性。如果像神经元这样的物理对象没有因果效力,那么 IIT 就是将意识等同于虚构,而不是具有效力的行为。此外,因果计算还不如放弃了因果的计算有力度。当 IIT 将意识等同于因果计算时,它就是将意识等同于次一等的计算。为什么意识应该低人一等?有没有关于意识的原理性洞察支撑这个可疑的主张?
物理因果的虚构性使得构建玄妙的“万物理论”变得棘手。我们必须先给出一个关于我们的界面的理论,以及它的各个层次的数据压缩和纠错。然后我们可以用这个理论来问,从我们在界面上看到的结构中,我们能否推断出关于客观实在的什么。如果我们不能推断出任何东西,那么我们就必须假设一个客观实在的理论,并预测它会如何呈现在我们的界面上。如果要用我们的理论作出经验性预测,并通过细致的实验进行验证,以上是常规的科学程序。我怀疑,如果我们在这项事业上取得成功,我们将会发现,我们对生命和非生命的区分并不是出于对实在本质的洞察,而是由我们的时空界面的局限造成的。一旦我们将界面的局限性考虑进来,我们将会找到对实在的统一描述,包括生命和非生命。我们还会发现,神经元网络是我们用来表示纠错编码器的符号之一。
感知-决策-行动循环
在感知界面理论中,我们可以用如图 1 所示自主体与世界的互动简单表示感知与行为的关联。图顶部的圆角框表示自主体之外的世界。我暂时不会声称对这个世界有任何了解。特别是,我不会假设它有空间、时间或对象。我只能说这个神秘的世界有许多可以变化的状态,不管它们是什么。就自主体本身来说,有一系列体验和行为,也用圆角框表示。自主体基于当前的体验,决定是否以及如何改变当前的行为选择。标记为“决策”的箭头表示了这个决定。自主体然后对世界执行其选择的行为,图中表示为标有“行动”的箭头。自主体的行为改变世界的状态。反过来世界又会改变自主体的体验,图中表示为标有“感知”的箭头。感知和行为就这样在“感知-决策-行动” (PDA) 的循环中关联到一起(在附录中有对此的数学描述)。
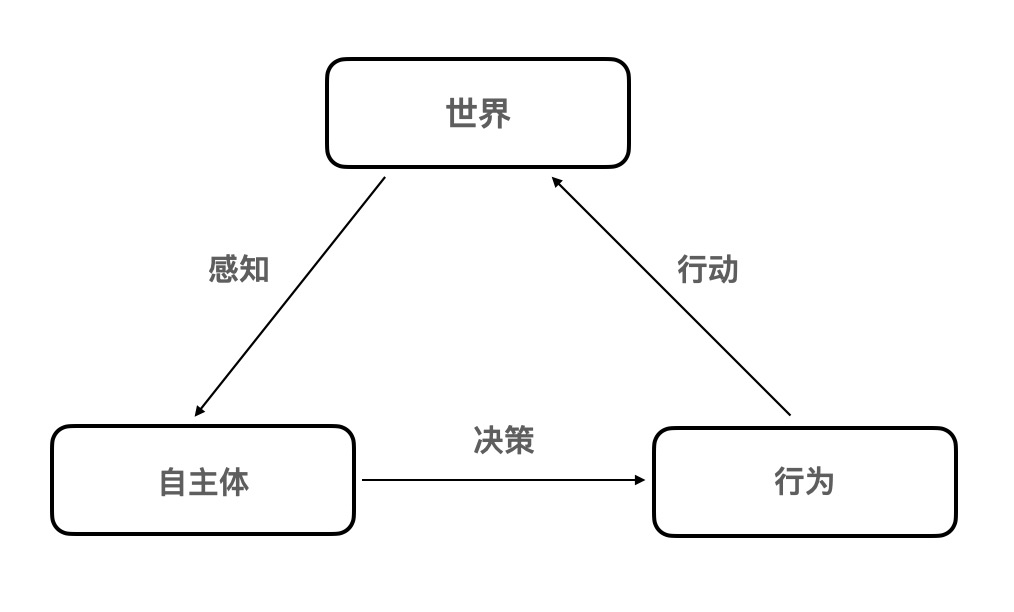
PDA 循环由进化的一个基本要素 — 适应度收益函数塑造。行为的适应性取决于世界的状态,但也取决于生物 (自主体) 及其状态。每当自主体对世界执行某种行为,它就会改变世界的状态,并获得适应度奖励 (或惩罚)。只有行为能获得足够适应度收益的自主体才能生存和繁衍。自然选择偏好 PDA 循环能正确调整适应度的自主体。对于这样的自主体,它的“感知”箭头传递了关于适应度的信息,它的体验呈现了这些关于适应度的信息。这些信息和体验都是关于适应度的,而不是关于世界的状态。自主体的体验变成了界面——不求完美,够用就行。它引导能收集足够适应度的行为,从而能存活足够长时间繁育后代。
经过一代又一代的无情选择,每个自主体都已经被塑造得选择的行为能带来理想的适应度收益。要成功繁育后代,自主体就必须采取能收集足够适应度的行为来繁育后代,感知、决策和行动必须相互协同。那些缺乏这种协同能力的自主体很可能会悲惨地英年早逝。具有这种协同能力的自主体,则会拥有能形成有用界面的感知,产生能与这个界面正确关联的行为。
体验和行为不是免费的。你的技能越多,你所需的卡路里就越多,所以选择压力会抑制自主体的技能数量。但如果你的技能太少,你可能会缺乏关于适应度的重要数据以及能提升适应度的关键行为。不同自主体会演化出不同的解决方案,以不同的方式来平衡选择的竞争压力。人类可能比甲虫拥有更多的嗅觉体验;熊又比人类拥有更多的嗅觉体验。没有完美的解决方案——只有可行的方案,让自主体在所处的小生境中生存下来。
但无论是怎样的解决方案,与相关的适应度收益的复杂性比起来,体验和行为的数目都是很少的。自主体感知的所有关于适应度的信息必须压缩成便于管理的大小和可用的格式,而且不能丢失关键信息。信息应该让自主体能发现和纠正错误。
例如,你在黄昏时沿着人行道散步,突然害怕地跳了起来。你环顾四周,寻找罪魁祸首,当你发现草丛中是一根浇花的水管时,你放心了。你的惊跳是由一条适应度信息触发的,但是纠错不充分——它错误地写着“蛇”。正因为这条消息没有在纠错上浪费时间,所以它很快送达了,并且你迅速采取行动以避免适应度受损。在最初的惊吓之后,一条纠错信息出现了:“别担心,只是水管。”你不必要的跳跃浪费了卡路里,压力诱发了肾上腺素的分泌,所以它略微损害了你的适应度。但从长远来看,这种快速且容易出错的信息通过降低致命咬伤的风险增加了你的适应度。如果你只依靠可靠但缓慢的信息,那么很可能有一天你会正确地得知“你刚刚被蛇咬了”。很对,但没什么帮助。
这说明对于适应度信息的压缩和纠错有多种解决方案。我们可以想见,自然选择已经形成了各种解决方案,以应对变化多端的适应性,并且单个生物也可能有多种解决方案,以应对不同的适应性需求。但我们也可以想见在不同物种之间会有类似的解决方案,因为在物种形成的过程中,进化通常会再利用而不是重新设计。在眼睛的蹩脚设计中我们就能看到再利用:通过眼睛晶状体的光必须穿透血管和中间神经元的遮挡,才能碰到视网膜后部的感光器。所有脊椎动物都是这样的,这表明它在脊椎动物进化的早期就出现了,并且从未被纠正过。这种蹩脚设计完全没有必要。头足类动物的设计就是正确的,比如章鱼和鱿鱼的光感受器就位于中间神经元和血管的前面。
从二维全息膨胀出三维
我们可以在图 11 的视觉示例中看到实时纠错。左边的两个黑盘上有白色的剪口。右边是这两个盘旋转后剪口对齐。突然间,你看到的不仅仅是有剪口的圆盘。你看到一条发光线漂浮在圆盘前面。你可以检查圆盘之间是否绘制了发光:用拇指盖住圆盘,发光就会消失。

你可以把这条发光的线看作你对擦除的纠正。这就好像你的视觉系统判断实际信息是一条直线,但是这条直线的一部分在传输过程中被抹去了。它通过用一条发光线填充缺口来纠错。这类似于对只能发送 000 和 111 两种消息的简单“汉明”码纠错。如果接收者收到比如说 101,那么它就知道有错误,中间的 1 被擦除了,所以它修复了擦除并得到消息 111。汉明码使用 3 比特发送 1 比特信息,因此它允许接收者检测和纠正单个擦除错误。
通过纠正黑盘图像中的擦除,你可以恢复一条消息:“圆盘前面的线。”还可以恢复另一条消息:“圆盘后面的线。”要得到这条消息,请将圆盘想象成白纸上的孔。你在透过这些孔看,在纸的后面看到一条线。请注意,当你看到这条线时,圆盘之间的线段不再发光,但你仍可以感觉到它在那里。
当你不看时,哪条线在那里?发光的还是不发光的?这个问题当然很蠢。当你不看时就没有线。你看到的线是你在更正擦除后恢复的信息。
让我们问另一个问题:当你在看时,你会看到哪条线?发光的还是不发光的?你不能确定。有时你会看到发光的线,有时看到不发光的线。但是你可以猜测概率。我更经常看到发光的线。我会说,我看到它发光的概率大约是 3/4,看到它不发光的概率约是 1/4。如果有人要求我用概率来表示这条线的“状态”(发光或不发光),我会为这条线写下一个“叠加”态,在其中,发光态的概率为 3/4,不发光态的概率为 1/4。这类似于我们之前在量子理论中遇到的叠加态。回想一下,根据量子贝叶斯理论,量子态并不描述即使没有人观察也存在的世界的客观状态,而是描述某个自主体的信念,即如果她采取行动,她会看到什么,或者,更严格地说,如果她进行测量,她会得到什么结果。
让我们进一步看看这个例子。在图 12 中,左侧有 4 个带切口的黑色圆盘。右边对这些圆盘进行了旋转,让切口对齐。突然间,你不仅仅看到带有切口的圆盘,你还可以看到 4 条发光线漂浮在圆盘前方。每条发光线似乎都在圆盘之间的空白处继续延伸。你可以再次检查是否是你创建了圆盘之间的发光线,用拇指覆盖两个圆盘,发光线消失了。

你的视觉系统纠正了 4 个擦除错误,创建了 4 条发光线。同时它也检测到了更高级别的编码信息:一个正方形。它接收不同抽象层次的信息——一维线和二维正方形。你的纠错可能同时涉及两个层次;正方形信息的证据增强了你的视觉系统对应该恢复被擦除线条的信心。
你的视觉系统还可以检测到另一种关于正方形的信息。再一次,把 4 个黑色圆盘想象成白纸上的孔洞,想象你正在透过这些洞看。你会看到纸的后面有一个正方形。当你这样作时,注意它的线条并没有发光。你确信这些线条是存在的,但是它们被白纸遮住了。
所以你可以从这个图中得到两条不同的关于正方形的信息。其中一条信息是前面的正方形,有发光的线条;第二条信息是后面的正方形,线条不发光。请注意,要么 4 条线都发光,要么都不发光。你永远不会同时看到两条发光的线和两条不发光的线。为什么?因为你的视觉系统已经将全部 4 条线组合成统一的信息:一个正方形。它将 4 条线“纠缠”在单个物体中,因此 4 条线必定是一样的。
现在进行这个例子的最后一步。图 13 的左边是 7 个有切口的黑色圆盘。右边对这些圆盘进行旋转,让切口对齐。突然你看到了 6 条发光的线条;你纠正了 6 处擦除的线条。
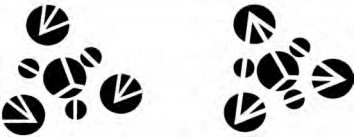
但是现在你会做更激进的事情:你把这些线纠缠成单个物体——一个四棱锥——在这个过程中,你创建了一个新的维度——深度。你用二维信息全息膨胀出三维。这个例子中的纠缠与创建三维空间的意识体验密切相关。请注意,有时你会看到顶角朝外的四棱锥,有时是顶角朝内的四棱锥。当你从一个四棱锥变换为另一个时,你逆转了你全息构建的三维深度关系——前面的线条变成了后面的线条,反之亦然。这些线条都纠缠为一个整体,有一个现象可以证实这一点,当四棱锥出现在圆盘前面时,它们都会发光,出现在圆盘后面时,它们都不再发光。
在量子理论中,马克·范拉姆斯东克、布莱恩·施温格等人的研究表明,时空由纠缠的丝线编织而成。我怀疑不仅仅是相似。我怀疑在我们的视觉例子中看到的叠加态、纠缠和三维全息膨胀与量子理论中研究的完全相同。时空不是独立于观察者的客观实在。它是由自然选择塑造的界面,用来传递适应度信息。在四棱锥的视觉例子中,我们看到这个时空界面以及纠错、叠加、纠缠和全息膨胀在起作用。
另一种将二维空间膨胀为三维空间的方法如图 14 所示。左边圆盘中每个点的亮度随机选择。你只能看到噪声。中间圆盘的亮度均匀,看起来是平的。右边圆盘中的亮度则是逐渐而系统地变化。现在奇迹发生了——你把圆盘膨胀成了球体。即使这些信息是二维的,你也可以将其全息膨胀成三维物体。

有时你膨胀出一个凸面,有时膨胀出一个凹面,如图 15 所示:你的视觉系统更喜欢让膨胀出的形状显得光线像是从顶上照射下来的。
除了膨胀亮度梯度外,你还会膨胀曲线,如图 16 所示。左边是有直线网格的圆盘,它看起来是平的。中间圆盘的线条略微弯曲,你会将它膨胀成球体。右边的曲线和亮度梯度结合在一起,你会将它膨胀成很逼真的球体。

我们从这些直线、正方形、立方体和球体的例子中学到了什么?按照标准的视觉科学的说法,这些例子向我们展示的是视觉系统是如何重建真实物体在客观时空中的真实形状。
而根据感知界面理论的说法,它们向我们展示的是完全不同的东西:视觉系统如何解码有关适应性的信息。没有客观时空,我们也不是在试图恢复时空中预先存在的物体的真实属性。相反,时空和物体只是传递适应性信息的编码系统。在刚刚看到的这些视觉例子中,我们发现自己把信息从二维膨胀成三维,这并不是表明客观实在是二维而不是三维的。相反,它们旨在挑战我们认为时空本身是客观实在的信念。这些例子有两个维度只是为了适合在纸上展示。
如果适应性信息被少量噪声损坏,系统有时可以纠错,就像我们看到的发光线条。如果噪声太多,比如像素具有随机亮度的圆盘,我们就无法纠错;我们看到的噪声没有清晰的适应性信息。
但是,如果亮度和轮廓传递了一致的信息,那么我们通常会将这些信息解码成三维形状的语言,这种语言是为引导适应性动作而量身定制的。例如,我们看到球体,就能知道该如何抓住它或避开它。我们看到苹果,就知道抓起和吃掉它可以增加我们的适应度;我们看到猎豹,就知道采取靠近它是不明智的。
总之,时空不是在生命萌芽前很久就已存在的古老剧场。它是我们临时创建的数据结构,用于搜寻和捕获适应度收益。像梨子和行星这样的物体,也不是在意识出现之前很久就已存在的古老舞台道具。它们也是我们创建的数据结构。梨子的形状是描述适应度收益的编码,并建议了我们可以采取的获取它们的行动。它的距离编码了我接近并抓取它的能量消耗。
参阅资料
推荐阅读
